Why Tensors? A Beginner's Perspective

Published

08 March 2022

I’ve been working through Leonard Susskind’s The Theoretical Minimum course, and one thing I’ve found interesting is the ubiquity of tensors - they seem to pop up everywhere in physics. I’ve been trying to build some intution behind what makes them so widely applicable, and I wanted to share my notes on this in the hopes that others might also find this useful. I’d also welcome any insights or corrections.

Most commonly, a tensor is defined as being anything that transforms like a tensor. Specifically, a tensor $T$ is a bunch of numbers, one for each coordinate (in whatever coordinate system you’re using), such that if you change coordinates from $x$ to $x’$, the components of $T$ (i.e., the numbers that make up $T$) transform according to the tensor transformation law.

\[T'^\nu = \frac{\delta x'_\nu}{\delta x_\mu}T^\mu\]

Where $\nu$ and $\mu$ label indices of $T’$ and $T$ (both of rank 1 - this isn’t the more general transformation law), respectively.

I don’t want to dig into this too much for now, because although this is the definition that tends to be the most useful in practice, I haven’t found it too helpful for building more intuition for where tensors come from. That said, this definition does point to something crucial - transformations.

Let’s start by asking the question - why would a transformation property be the defining property of an object, i.e., why would we want some object $T$ (a tensor) to transform if the underlying coordinates used to define that object change?

The idea here is that we want to represent an object that doesn’t depend on the coordinates that someone chooses to make measurements. If I make measurements in polar coordinates and you make them in cartesian coordinates, we should both be able to perform calculations and come up with the same result - the laws of physics should not depend on systems of coordinates. So if I make some measurements in my coordinate system and then change those coordinates a bit, then my measurements, the components of $T$, should change in a way such that they always represent the same object.

Figure 1. A point can be represented in terms of its cartesian coordinates, $x_0$ and $y_0$, or polar coordinates, $r_0$ and $\theta_0$. The coordinates are different depending on what coordinate system is used, but any set of physical laws but produce the correct results in every coordinate system.

Think of converting units. Suppose that you weigh an object and find that it weights 100 kilograms, and you’d like to convert this to pounds. If we think of the units (kilograms/pounds) as a coordinate, then in a way we are changing the coordinate system used to make our measurement. However, converting units obviously doesn’t make the object lighter, so to ‘compensate’ the fact that pounds are a smaller unit than kilograms, we don’t just leave the 100 there - we multiply it to make sure that the fundamental measurement doesn’t change. This gives some idea of how transformations help ensure that we are coordinate invariant.

So by looking at the tensor transformation law given above, it seems reasonable to guess that there is some notion of sameness involved. But why that specific transformation law - why must tensors transform in that way in order to preserve whatever object the tensor represents?

It turns out that there is another definition of tensors that is equivalent to the one given above. Specifically, a tensor is something that takes a bunch of vectors and spits out a real number. This still sounds fairly abstract, so let’s drill into a few examples to see why converting vectors into real numbers might be a useful thing to do.

Let’s start with measurements of distance. Suppose that you see an object move from position $x_0$ at $t_0$ to $x_1$ at $t_1$. From your perspective, $dt$, the change in time is $t_1 - t_0$, and $dx$, the change in the position of the object, is $x_1 - x_0$. We can build a vector out of these measurements: $\begin{bmatrix} dx \ dt \end{bmatrix}$.

Now suppose that there’s another observer also looking at that object, but that observer is moving at nearly the speed of light. When this observer tries to build a vector recording their measurements, they’ll record a much smaller value of $dt$, since clocks slow down as you approach the speed of light, and also a smaller value of $dx$ since distances contract.

The problem for us is that we want a way of formulating the laws of physics that can be used to give the same results regardless of the frame of reference measurements are made in. This is tricky - since two observers can observe completely different values of $dx$ and $dt$ for the same object!

There’s an interesting result in special relativity that says that for any measurements of $dx$ and $dt$, although two observers might get completely different values, they’ll always agree on the value of $dx^2 - dt^2$. We call this value $ds$, or the proper distance traversed by the object, and it is invariant in all frames of reference. So if we come up with laws that only depend on $ds$, then they will also be valid in all frames of reference!

Electromagnetism is another interesting example of a case where observers can record completely different measurements depending on their frame of reference. For instance, think about a magnet moving relative to a wire. From the point of view of the wire, the moving magnet creates an electric field, which creates a force on the wire, producing a current.

On the other hand, from the point of view of the magnet, the magnetic field created by the magnet interacts with the moving wire to produce a force on the wire, creating a current. So depending on the frame of reference, it’s either an electric or magnetic field that’s doing the work. The wire only experiences an electric field, whereas the magnet thinks that it’s just a magnetic field.

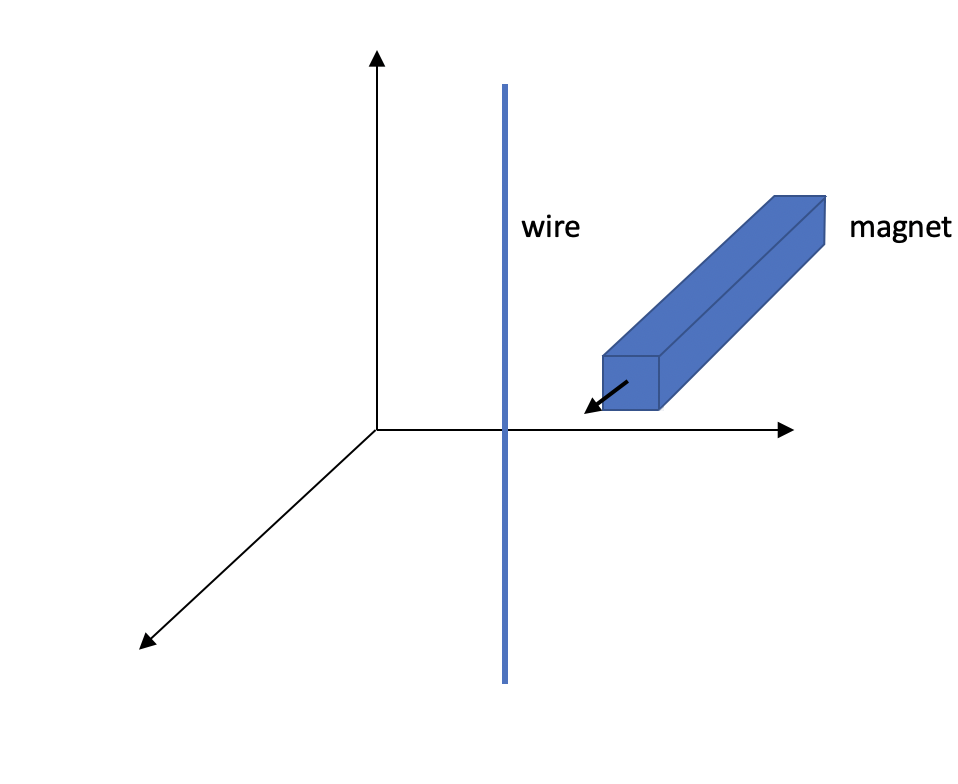
Figure 2. An example of how different physical observers can interpret the same phenomena in different ways. A moving magnet thinks that its magnetic field is interacting with a moving wire to produce a current. The wire, on the other hand, would say that the moving magnet creates an electric field, which creates a current.

Again, it turns out there’s a way to bring these two different descriptions of the same reality together. It turns out that $\textbf{E}^2 - \textbf{B}^2$, where $\textbf{E}$ is the electric field and $\textbf{B}$ is the magnetic field, is always the same in every coordinate frame.

So there’s the same pattern again. Observers can record different measurements of time and distance, but agree on the value of $ds$. Observers can record different measurements of the electric and magnetic fields, but all agree on the value of $\textbf{E}^2 - \textbf{B}^2$. There are more examples of this - energy and momentum, and the metric tensor - just to name a few.

This is the core problem that tensors allow us to solve - they represent a rule that maps vectors, or sets of ‘related’ measurements (for our purposes), to something called a scalar - a number that all observers agree on. A tensor links the components of those vectors to something that is more fundamental. We can then build physical laws that take this property into account, and these laws will then be applicable in all frames of reference.

Introducing some notation, we represent a tensor $T$ as a map between a bunch of vectors $V$ to a scalar, which is a real number:

\[T : V \times V \times \dots \to \textbf{R}\]

We’re still missing one key piece of the puzzle. It just so happens that most mappings between vectors and scalars that we find in physics are linear. This completes the definition of tensors - they aren’t just any rule for taking vectors and spitting out scalars, but they are also linear. This property has really interesting implications for how we work with tensors.

Let’s start with our definition of a tensor - a linear rule for mapping a set of vectors to a real number. For now, let’s just consider the case where $T$ just ‘takes’ two vectors, though the following discussion will apply to any number of input vectors. It helps to think of $T$ as a machine that takes two vectors and spits out a real number.

Now let’s try to build a new machine given the one we already have, $T$. Let’s call this new machine $T’$. The way this machine will work is that when we first build it, we’ll ‘store’ or ‘hide’ some vector, let’s call it $V_1$, inside it. It also has its own copy of $T$.

Then, whenever this machine is given another vector (of type $V$), let’s call this vector $V_2$, it will just take $T$, feed it $V_1$ (which was hidden inside $T’$) and $V_2$. $T$ takes two vectors, so it will output a scalar, which $T’$ will then output as well.

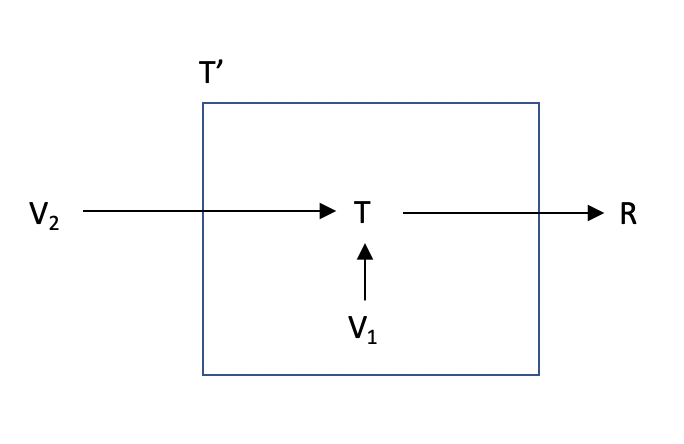
Figure 3. Given $T$, we can construct a new tensor $T'$ that takes in a single vector V instead of two vectors.

So starting from $T$, a machine to map two vectors into a scalar, we now have built a new machine $T’$ that maps a single vector into a scalar. Internally, this new machine is just using $T$ and a hidden vector, but from the outside, it looks like something new - it takes a single vector and maps it to a scalar. Which is the definition of a tensor! So starting from a tensor that took two parameters, we have constructed a new tensor that takes a single parameter.

There’s a nice way to categorize tensors. The original tensor, $T$, is considered a (2, 0) tensor since it takes two arguments. The new tensor we constructed is called a (1, 0) tensor. So just to recap:

\[T : V \times V \to \textbf{R}\] \[T' : V \to \textbf{R}\]

But what about the second number in that representation - where’s that 0 coming from? It turns out that the new tensor we built, the (1, 0) tensor, is an element of a vector space - so it is a vector. A new kind of vector, that is different from the kinds of vectors that $T$ takes - let’s call it $U$. So $U$ is two things: it is a tensor ($V \to \textbf{R}$), and it is also a vector.

\[U : V \to \textbf{R} \tag{1}\]

So far what we’ve done is taken $T$ and used it to build a $U$ vector. But what does $U$ have to do with $V$ and $T$?

Now comes the crucial step - the vectors that $T$ consumes, $V$, can also be thought of as a rule that can take a $U$ vector and map it to a scalar by applying itself to it! So a $V$ can take a $U$, use equation $(1)$ and just feed itself as input into the $U$, then output the scalar. So $V$, which was a vector, is also a tensor (i.e. a map between $U$ and $R$):

\[V : U \to \textbf{R} \tag{2}\]

So $V$ takes a $U$ - which is a recipe to map a $V$ into a scalar - and then applies it to itself, giving a scalar. This is also a tensor! This would be considered a (0, 1) tensor - as it maps a single $U$ vector to a scalar.

There’s a symmetry between $(1)$ and $(2)$. Given a $U$, we can convert it to a $V$, and vice versa. $U$ is called a dual vector or a covector of $V$.

This symmetry leads us to a final modification in the definition of tensors. Not only can a tensor take vectors $V$ as input, but also covectors. So any tensor $T$ is a linear map between a bunch of vectors and covectors to a scalar:

\[T : V \times V \times \dots \times U \times U \times \dots \to \textbf{R}\]

Lastly, it turns out that any tensor - a linear map from vectors to scalars - also follows the transformation laws given at the beginning of this post. So starting from two requirements:

We’ve built up a way of systematically categorizing these mappings - or tensors, with the nice property that even vectors can be considered tensors and tensors can be considered vectors. This is what makes tensors so powerful - they take a fairly small set of ‘requirements’ and provide a way to manipulate objects that match those requirements (through the tensor transformation laws), and also provide a way to build and decompose tensors from other tensors - making the abstraction all the more useful, as these same transformation laws can be used again and again.