Why Are Sines and Cosines Used For Positional Encoding?

One of the earliest steps in any neural network operating on sequences is position encoding - augmenting a sequence of input vectors so that the vectors also encode information about their position in the sequence. Many of the most commonly used schemes for doing this involve adding or multiplying these vectors by sinusoidal functions, and this can be a bit surprising - at first glance, sines and cosines are unlikely to have much to do with encoding positions.

This post attempts, in an elementary way, to build some intuition for why sinusoidal functions can be useful ways to represent position information. It does so in the context of Transformer networks and RoPE (Rotary Position Embedding), which happens to be the position encoding scheme used in Meta’s LLaMA model.

Transformers and Self-Attention

Let’s start with a brief (and simplified) review of the self-attention operation in Transformer networks. For each input vector $\mathbf{x}$ (which represents some token), we calculate three new vectors - the query $\mathbf{q}$, key $\mathbf{k}$, and value $\mathbf{v}$. Then, we output the following:

\[\mathbf{x_{out}} = (\mathbf{q}\cdot\mathbf{k_1})\mathbf{v_1} + (\mathbf{q}\cdot\mathbf{k_2})\mathbf{v_2} + \ldots + (\mathbf{q}\cdot\mathbf{k_n})\mathbf{v_n}\]

The idea is that the dot product between two vectors should give us some measure of how similar or interesting those vectors are to each other. So for some input vector $\mathbf{x}$, we first calculate a $\mathbf{q}$, and then calculate dot products with all other key vectors $\mathbf{k_1}, \mathbf{k_2}, \cdots, \mathbf{k_n}$ in the sequence to determine to what extent those vectors should influence the output we generate for $\mathbf{x}$. Finally, instead of just directly multiplying the results of the dot products by the $\mathbf{x_n}$ vectors, we multiply by their respective $\mathbf{v}$ vectors instead.

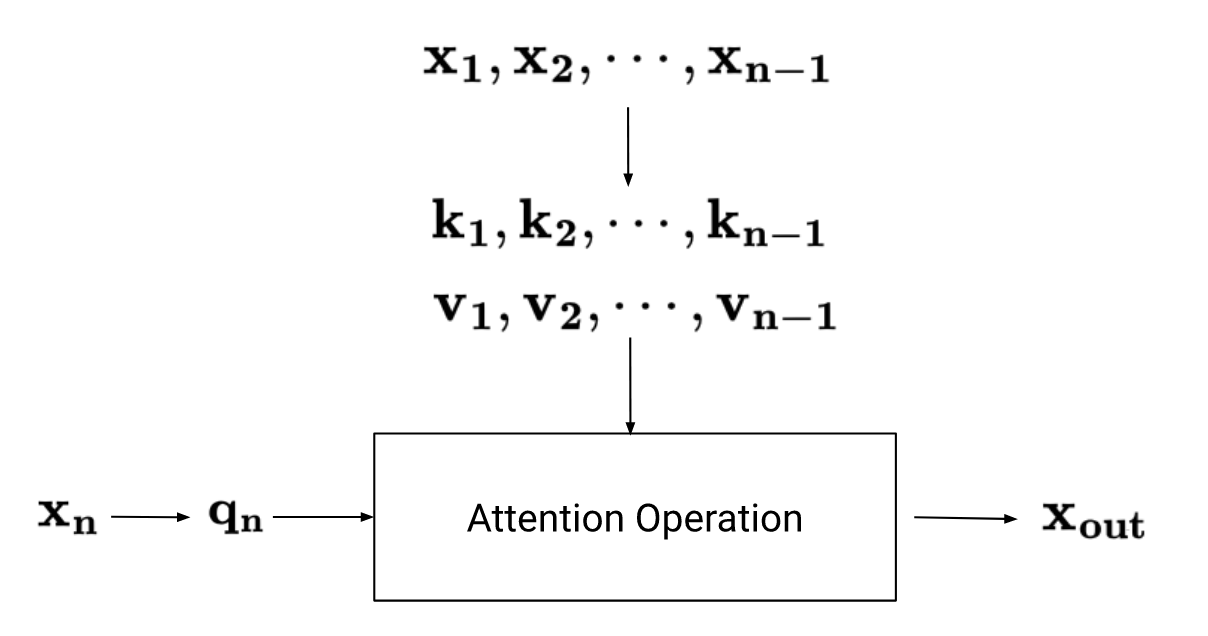
One shortcoming of this approach is that it doesn’t account for positions - two vectors will have the same dot product, regardless of how close they are to each other in the input sequence. What we want is a way to modify each vector in a way that incorporates information about its position.

Encoding Positions

To make things simpler, let’s assume that $\mathbf{x_m}$, which is some input vector that occupies position $m$, is a two dimensional vector. Then, we can represent it as a complex number:

\[x_m = |x_m|e^{i\theta_m}\]

Let’s define $f(x, m)$ as a function that takes a vector (represented as a complex number) and its position, and modifies the vector in a way that incorporates information about its position in the input sequence.

What properties would we like this function $f$ to have? Suppose that we have two vectors, one at position $m$ and one at position $n$. When we apply $f$ to both vectors to encode position information and then take the dot product of these two vectors (as part of the attention operation discussed earlier), we’d like the result to depend on the distance between the two vectors, i.e., $m - n$, and not on $m$ and $n$ themselves. So we’d like:

\[f(x_m) \cdot f(x_n) = g(x_m,x_n, m - n) \tag{1}\]

So $f$ should modify the original vectors in a way that when we take the product of the results, we end up getting a function that depends on the difference of the position parameters $m$ and $n$.

Exponentials

Note that the exponential function has a property that seems similar to what we want:

\[e^me^n = e^{m+n}\]

Continuing down this path - now we don’t want $f$ to just multiply $x_m$ by $e^m$, since that would cause the magnitude of $f$ to grow very quickly with position (i.e, with $m$). Instead, let’s try multiplying by $e^{im\theta}$ since its magnitude is unity - we won’t cause the magnitude of the vector to change. Our candidate $f$ is:

\[f(x_m, m) = x_{m}e^{im\theta}\]

We’ve also introduced a frequency parameter, $\theta$, which isn’t necessary at this point but will turn out to be useful later.

One question is - why are we trying out multiplication, as opposed to having $f$ be some more complicated function of $x$ and $m$? The intuition here goes back to the structure of Transformer networks - since the $\mathbf{q}$, $\mathbf{k}$, and $\mathbf{v}$ vectors are all linear transformations of the input vectors, the idea is that maybe if $f$ is a linear transformation of its input, it’ll be easier for the network to learn.

Now that we have a candidate for $f$, let’s verify that it really does satisfy property $(1)$. The dot product of two vectors represented as complex numbers is:

\[x_m \cdot x_n = \Re[x_{m}x^\star_n]\]

Where $\Re(x)$ represents the real part of $x$. If we apply $f$ to both $x_m$ and $x_n$, then this becomes:

\[\begin{align} f(x_m) \cdot f(x_n) &= \Re[x_{m}x^\star_{n}e^{i(m - n)\theta}] \\ &= \Re[|x_m||x_n|e^{i(\theta_m - \theta_n + [m - n]\theta)}] \\ &= |x_m||x_n| \cos(\theta_m - \theta_n + [m - n]\theta)\end{align}\]

Which has the property we wanted - the result is only a function of $m - n$, and not of $m$ or $n$ by themselves.

From Exponentials to Sinusoidal Functions

So now we have a candidate for $f$ when $\mathbf{x}$ is a complex number. What about the case where $\mathbf{x}$ isn’t represented as a complex number, but as a vector of two real numbers instead? In that case, we can use the fact that multiplying a complex number by $e^{i\theta}$ is the same as multiplying its components by a rotation matrix:

\[\begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}\]

So far we’ve assumed that $\mathbf{x}$ only has two dimensions. It turns out that we can easily extend this idea to the general case - we just break up the dimensions into pairs, and apply the two dimensional transformation to each pair.

This leads to another issue. Recall that the idea behind making $f$ linear was that the network should be able to easily represent vectors at different positions. But since $f$ is defined as a multiplication by a periodic function, it’ll actually lead to the same representation for points at varying distances. Making $\theta$ really large would allow the network to easily distinguish between positions closer together but not those that are farther apart, and making it small would lead to the opposite problem - positions close to one another might not lead to enough of a change in $f$ to allow the network to easily distinguish them.

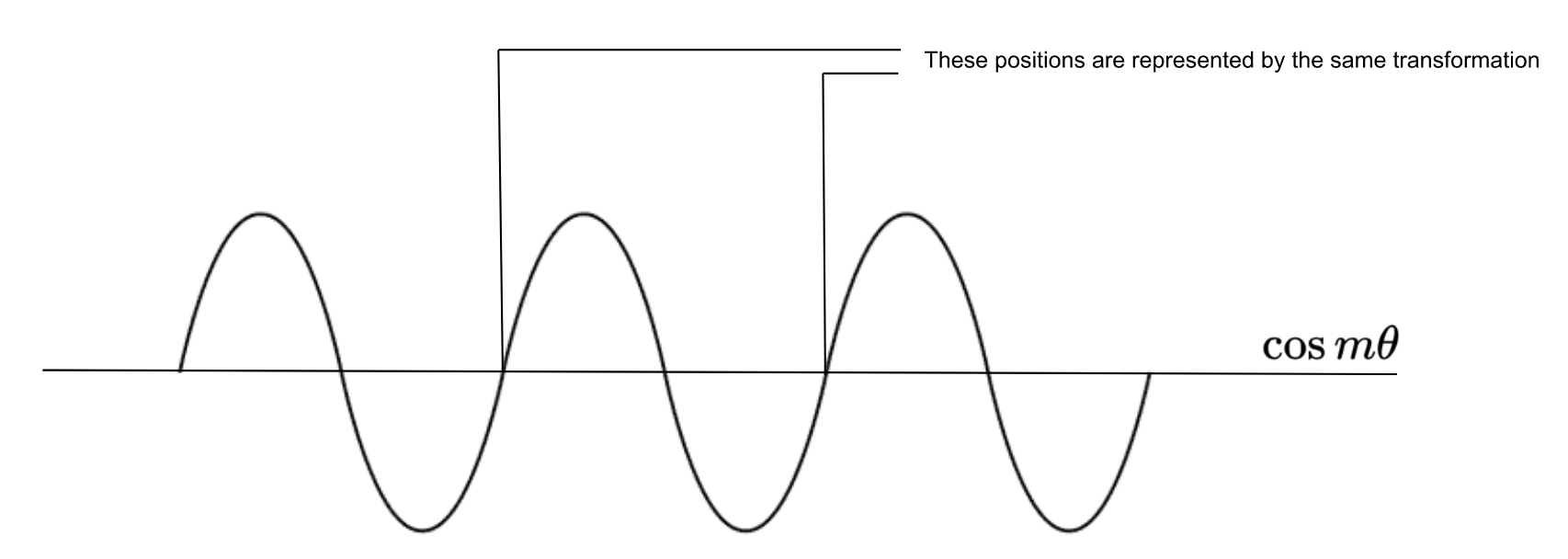
One way to deal with this is to use different values of $\theta$ for each pair of dimensions. So some dimensions will encode shorter distance information, and some will encode longer distance information. Putting it all together, we get the following transformation:

\[f(\mathbf{x}, m) = \mathbf{x}\begin{pmatrix} \cos m\theta_1 & -\sin m\theta_1 & 0 & 0 & \cdots & 0 & 0 \\ \sin m\theta_1 & \cos m\theta_1 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos m\theta_2 & -\sin m\theta_2 & \cdots & 0 & 0 \\ 0 & 0 & \sin m\theta_2 & \cos m\theta_2 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos m\theta_{d/2} & -\sin m\theta_{d/2} \\ 0 & 0 & 0 & 0 & \cdots & \sin m\theta_{d/2} & \cos m\theta_{d/2} \end{pmatrix}\]

In summary - fairly simple considerations around properties we’d like the dot product to have (i.e., only being a function of $m - n$) and a preference for linear transformations leads to an effective positional embedding scheme that uses sinusoidal functions and generalizes to any number of dimensions - which is quite remarkable.